3  Model setup & priors

Author

Sebastian Weber -

Show R setup 
library(ggplot2)
library(dplyr)
library(knitr)
library(brms)
library(posterior)
library(ggdist)
library(bayesplot)
library(tidybayes)
library(forcats)
library(RBesT)
library(here)
# instruct brms to use cmdstanr as backend and cache all Stan binaries
options(brms.backend="cmdstanr", cmdstanr_write_stan_file_dir=here("_brms-cache"))
# create cache directory if not yet available
dir.create(here("_brms-cache"), FALSE) 
set.seed(593467)
theme_set(theme_bw(12))

Within the Bayesian regression modeling in Stan framework brms priors are required to perform inference. This introductory material is intended to provide some pragmatic considerations on how to setup priors and point readers to material to follow-up on. The case studies themselves provide details on setting up priors for the respective problem. By default these priors have been chosen to have minimal impact on the posterior whenever appropriate and also ensure stable numerical inference. As a consequence, the results from the case studies will resemble respective Frequentist model results in most cases. Nonetheless, priors are defined explicitly for all models, since these are an integral part of any Bayesian analysis. This can be easily seen by considering Bayes rule to obtain the posterior:

\[ p(\theta | y) = \frac{p(y|\theta) \, p(\theta)}{p(y)} \propto p(y|\theta) \, p(\theta)\]

The marginal likelihood term \(p(y)\) can be dropped, since this is merely a normalization constant given that we condition the inference on the observed data \(y\). What is left is hence the product of the likelihood \(p(y|\theta)\) multiplied by the prior \(p(\theta)\). The posterior information on \(\theta\) is hence provided equally by likelihood and prior.

From a practical perspective one may ask under which circumstances it actually matters which prior we set. In many cases the posterior is dominated by the data, which means that the likelihood term \(p(y|\theta)\) is much larger than the prior term \(p(\theta)\). This is the case for most case studies. It is tempting to drop the prior in these cases and not worry about it. However, this is not recommended as it is in many instances of interest to study a model with small sample sizes eventually (by applying the model to subsets, increasing model complexity, etc.). Another practical aspect is the numerical stability and quality of the Markov Chain Monte Carlo (MCMC) sample we obtain from Stan. Without a prior the inference problem becomes much harder to solve. That is, the Markov Chain Monte Carlo (MCMC) sampler Stan has to consider the full sampling space of the prior. Dropping the prior entirely implies an improper prior on the sampling space which becomes un-countably infinitely large. Rather than dropping the prior entirely we strongly recommend to consider so-called weakly informative priors. While no formal definition is given in the literature, these priors aim to identify the scale of parameters. This requires a basic understanding of the parameters for which priors are being defined. Thus, a prior can only be understood in the overall context of the likelihood, parametrization and problem at hand (see also Gelman, Simpson, and Betancourt 2017). For most statistical analyses this means to consider the endpoint and the applied transformations.

To just get started with brms one may choose to not specify priors when calling brm. Doing so will let brms provide in most cases reasonable default priors. These default priors are intended to avoid any influence on the calculated posterior. Hence, the results are fully data driven and will be very close to the respective Frequentist maximum likelihood inference result. However, the default prior is not guaranteed to stay stable between releases and can thus change whenever the brms version changes.

Given that any Bayesian analysis requires a prior, we recommend to always explicitly define these - even if these just repeat the default prior from brms, which one can easily obtain. Here we use as example binomially distributed data (responder in a control arm) and we use the simplest possible model, which will pool the information across the different studies (in practice one would allow for between-trial heterogeneity):

model <- bf(r | trials(n) ~ 1, family=binomial)

## with brms >= 2.21.0 we can  directly write... 
## default_prior(model, data=RBesT::AS)

## a workaround is to create an empty brms model and obtain the
## defined prior like
prior_summary(brm(model, data=RBesT::AS, empty=TRUE)) |> kable()
prior class coef group resp dpar nlpar lb ub tag source
student_t(3, 0, 2.5) Intercept default

Note that we have defined first the model via the bf call. This defines the linear predictor and the likelihood using the family argument of bf. We recommend to always explicitly do this step first as it defines the likelihood and the model parametrization in one step. Choosing these is a critical first step in defining the model and, most importantly, the chosen priors can only be understood in the context of the model (likelihood and parametrization) (see Gelman, Simpson, and Betancourt 2017).

Rather than running the model with no explicit prior definition we encourage users to explicitly define the priors used for the analysis - even if these are simply the default priors:

model_def <- bf(r | trials(n) ~ 1, family=binomial)
model_prior <- prior(student_t(3, 0, 2.5), class=Intercept)

fit <- brm(model_def, data=RBesT::AS, prior=model_prior, seed=467657, refresh=0)
Running MCMC with 4 sequential chains...

Chain 1 finished in 0.0 seconds.
Chain 2 finished in 0.0 seconds.
Chain 3 finished in 0.0 seconds.
Chain 4 finished in 0.0 seconds.

All 4 chains finished successfully.
Mean chain execution time: 0.0 seconds.
Total execution time: 0.8 seconds.
fixef(fit)
           Estimate Est.Error      Q2.5     Q97.5
Intercept -1.106901 0.1062962 -1.314909 -0.907616

The provided default prior is indeed not informative, as can be seen by comparing the posterior estimate to the respective Frequentist fit from glm:

fit_freq <- glm(cbind(r, n-r) ~ 1, data=RBesT::AS, family=binomial)
## intercept estimate
coef(fit_freq)
(Intercept) 
   -1.11165 
## standard error estimate
sqrt(vcov(fit_freq)[1,1])
[1] 0.1022971

In this case the data with a total of 513 subjects dominates the posterior. Nonetheless, it is illustrative to consider in more detail the prior here as an example. Importantly, the intercept of the model is defined on the logit scale of the response probability as it is common for a standard logistic regression. The transformation changes the scale from the interval 0 to 1 to a new scale which covers the entire space of reals. While formally very large or very small logits are admissible, the range from 5% to 95% response rate corresponds to -3 to 3 on the logit space approximately. Thus, logit values smaller or greater than these values would be considered extreme effects.

When defining a prior for a model we would typically want to compare different choices of the prior to one another. As example prior for the intercept only model we may compare here three different priors: (i) a very wide prior \(\mbox{Normal}(0,10^2)\), (2) the default brms prior and (3) the density \(\mbox{Normal}(0,2^2)\) as used as default prior in RBesT for this problem. In a first step we sample these priors and assess them graphically. We could use brms to sample these priors directly with the argument sample_prior="only", but we instead use basic R functions for simplicity:

Show the code 
num_draws <- 1E4
priors_cmp <- tibble(case=c("wide", "brms", "RBesT"),
                     density=c("N(0,10^2)", "S(3, 0, 2.5^2)", "N(0, 2^2)"),
                     prior=rvar(cbind(rnorm(num_draws, 0, 10),
                                      rstudent_t(num_draws, 3, 0, 2.5),
                                      rnorm(num_draws, 0, 2))))

kable(priors_cmp, digits=2)
case density prior
wide N(0,10^2) -0.2203 ± 9.9
brms S(3, 0, 2.5^2) 0.0058 ± 4.4
RBesT N(0, 2^2) 0.0104 ± 2.0
Show the code 
priors_logit <- priors_cmp |>
    ggplot(aes(y=case, xdist=prior)) +
    stat_slab() +
    xlab("Intercept\nlinear predictor") +
    ylab(NULL) +
    labs(title="Prior logit scale") +
    coord_cartesian(xlim=c(-30, 30))

priors_response <- priors_cmp |>
    ggplot(aes(y=case, xdist=rdo(inv_logit(prior)))) +
    stat_slab() +
    xlab("Intercept\nresponse scale") +
    ylab(NULL) +
    labs(title="Prior response scale") +
    coord_cartesian(xlim=c(0, 1))

bayesplot_grid(priors_logit, priors_response, grid_args=list(nrow=1))

As one can easily see, the wide prior has density at very extreme logit values of -20 and 20. In comparison, the brms and the RBesT default prior place most probability mass in the vicinity of zero. While the wide prior may suggest to be very non-informative it’s meaning becomes clearer when back transforming to the original response scale from 0 to 1. It is clear that the wide prior implies that we expect extreme response rates of either 0 or 1. In contrast, the RBesT default prior has an almost uniform distribution on the 0 to 1 range while the default brms prior has some “U” shape. 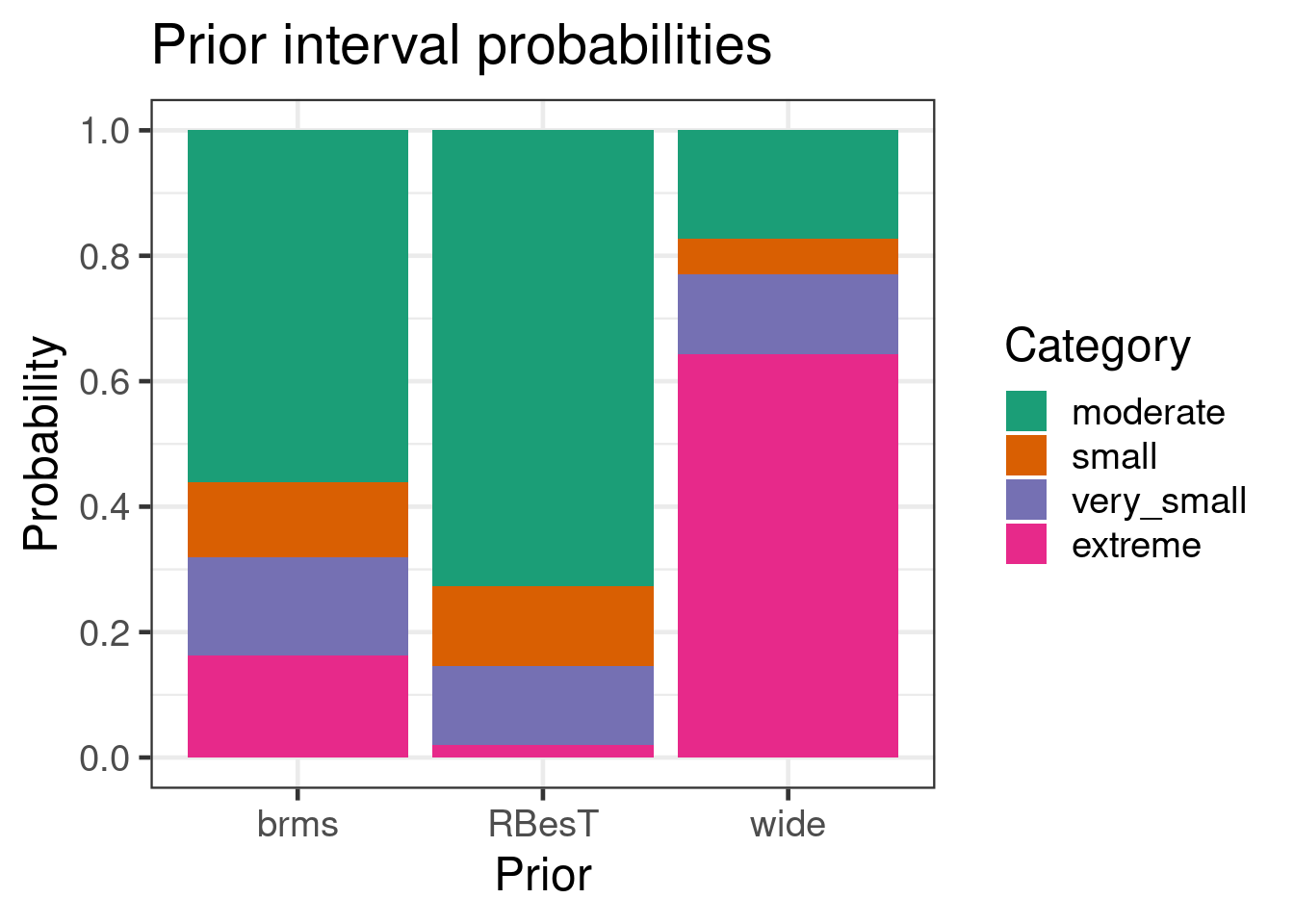To now further discriminate these priors a helpful concept is to consider interval probabilities for pre-defined categories. The definition of cut-points of the categories is problem specific, but can be defined with usual common sense for most endpoints. The critical step here is in defining these categories and documenting these along with the analysis. Here we categorize the response as extreme 0-1% & 99-100%, very small 1-5% & 95-99%, small 5-10% & 90-95% and moderate for the remainder. Comparing then these priors gives:

Show the code 
response_category <- function(r) {
    fct_rev(cut(pmin(r, 1-r), c(0, 0.01, 0.05, 0.1, 0.5), labels=c("extreme", "very_small", "small", "moderate")))
}

priors_cmp |> unnest_rvars()|> 
    ggplot(aes(x=case, fill=response_category(inv_logit(prior)))) +
    geom_bar(position="fill") +
    xlab("Prior") +
    ylab("Probability") +
    labs(title="Prior interval probabilities", fill="Category") +
    scale_y_continuous(breaks=seq(0,1,by=0.2)) +
    theme(legend.position="right")

Show the code 
mutate(priors_cmp,
       prior_response=rfun(inv_logit)(prior),
       summarise_draws(prior_response,
                       extreme=~100*E(.x < 0.01 | .x > 0.99),
                       very_small=~100*E( (0.01 <= .x & .x < 0.05) | (0.95 < .x & .x <= 0.99) ),
                       small=~100*E( (0.05 <= .x & .x < 0.1) | (0.9 < .x & .x <= 0.95) ),
                       moderate=~100*E( (0.1 <= .x & .x < 0.9) )
                       )) |>
    select(case, density, extreme, very_small, small, moderate) |>
    kable(digits=1, caption="Interval probabilities per prior given in percent")
Interval probabilities per prior given in percent
case density extreme very_small small moderate
wide N(0,10^2) 64.2 12.8 5.7 17.3
brms S(3, 0, 2.5^2) 16.3 15.7 12.0 56.1
RBesT N(0, 2^2) 2.2 11.2 13.0 73.6

It is apparent that the seemingly non-informative prior “wide” is in fact an informative prior implying that the expected response rates are extreme. This is the consequence of transforming to the logit scale.

In practice one would most certainly not fit the intercept only model, which pools the information. The RBesT::AS data set is in fact the standard example for the use of historical control data.

kable(RBesT::AS)
study n r
Study 1 107 23
Study 2 44 12
Study 3 51 19
Study 4 39 9
Study 5 139 39
Study 6 20 6
Study 7 78 9
Study 8 35 10

To use this data as historical control data one uses instead of the intercept only model a random intercept model, which casts this into a meta-analtyic model:

model_meta_def <- bf(r | trials(n) ~ 1 + (1 | study), family=binomial)
model_meta_prior <- prior(normal(0, 2), class=Intercept) +
    prior(normal(0, 0.5), class=sd, coef=Intercept, group=study)

fit_meta <- brm(model_meta_def, data=RBesT::AS, prior=model_meta_prior,
                seed=982345, refresh=0, control=list(adapt_delta=0.95))
Running MCMC with 4 sequential chains...

Chain 1 finished in 0.2 seconds.
Chain 2 finished in 0.2 seconds.
Chain 3 finished in 0.2 seconds.
Chain 4 finished in 0.2 seconds.

All 4 chains finished successfully.
Mean chain execution time: 0.2 seconds.
Total execution time: 1.4 seconds.
summary(fit_meta)
 Family: binomial 
  Links: mu = logit 
Formula: r | trials(n) ~ 1 + (1 | study) 
   Data: RBesT::AS (Number of observations: 8) 
  Draws: 4 chains, each with iter = 2000; warmup = 1000; thin = 1;
         total post-warmup draws = 4000

Multilevel Hyperparameters:
~study (Number of levels: 8) 
              Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
sd(Intercept)     0.34      0.17     0.04     0.73 1.01     1186     1066

Regression Coefficients:
          Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
Intercept    -1.11      0.17    -1.47    -0.75 1.00     1622     1731

Draws were sampled using sample(hmc). For each parameter, Bulk_ESS
and Tail_ESS are effective sample size measures, and Rhat is the potential
scale reduction factor on split chains (at convergence, Rhat = 1).

The meta-analytic model is generative in the sense of allowing to predict the mean response rate for future studies by way of the hierarchical model structure. Now the importance of the prior on the overall intercept becomes more relevance as the information from each study is discounted through the random effects model leading to less data to estimate the parameter in comparison to the full pooling model. However, the key parameter in this model is the between-trial heterogeneity parameter. In the example a half-normal prior with scale 1 is used (brms knows that the parameter must be positive and hence truncates the prior at zero automatically). This distribution of a half-normal density has been studied extensively in the literature and found to be a robust choice in a wide range of problems. For this reason, it is a very rational choice to use this prior in the current (and future) analyses. The choice of the scale of 0.5 is often referred to as a conservative choice in this problem while 1 is a very conservative choice and 0.25 a less conservative choice. A complication with the hierarchical model is that \(\tau\) itself implies a distribution. To simplify this, we first consider the case of a known between-trial heterogeneity parameter and study what this implies. For a known \(\tau\) the range of implied log odds can be characterized by the respective 95% probability mass range given by \(2 \cdot 1.96 \, \tau\), which is interpret-able as the largest log odds ratio. Recalling that the between-study heterogeneity parameter controls the (random) differences in the logits of response rates between studies, it is helpful to consider the distribution of implied log odds ratios between random pairs of two studies. These differences (log odds ratios) have a distribution of \(\mbox{Normal}(0, (\sqrt{2} \, \tau)^2)\). Considering the absolute value of these differences, the distributions becomes a half-normal with scale \(\sqrt{2} \, \tau\), which has it’s median value at \(1.09 \, \tau\). This results for a range of values of \(\tau\) on the respective odds scale to:

tau largest_odds_ratio median_odds_ratio
0.000 1.000 1.000
0.125 1.632 1.146
0.250 2.664 1.313
0.500 7.099 1.725
1.000 50.400 2.974
1.500 357.809 5.129
2.000 2540.205 8.846

In (Neuenschwander and Schmidli 2020) suggest the categorization of the between-study heterogeneity \(\tau\) parameter the values of \(1\) for being large, \(0.5\) substantial, \(0.25\) moderate, and \(0.125\) small. Considering these with the table above qualifies these categories as plausible. An alternative approach to the categorization is to consider what is an extreme value for \(\tau\) (like unity) and then choose the prior on \(\tau\) such that a large quantile (like the 95% quantile) corresponds to this extreme value.

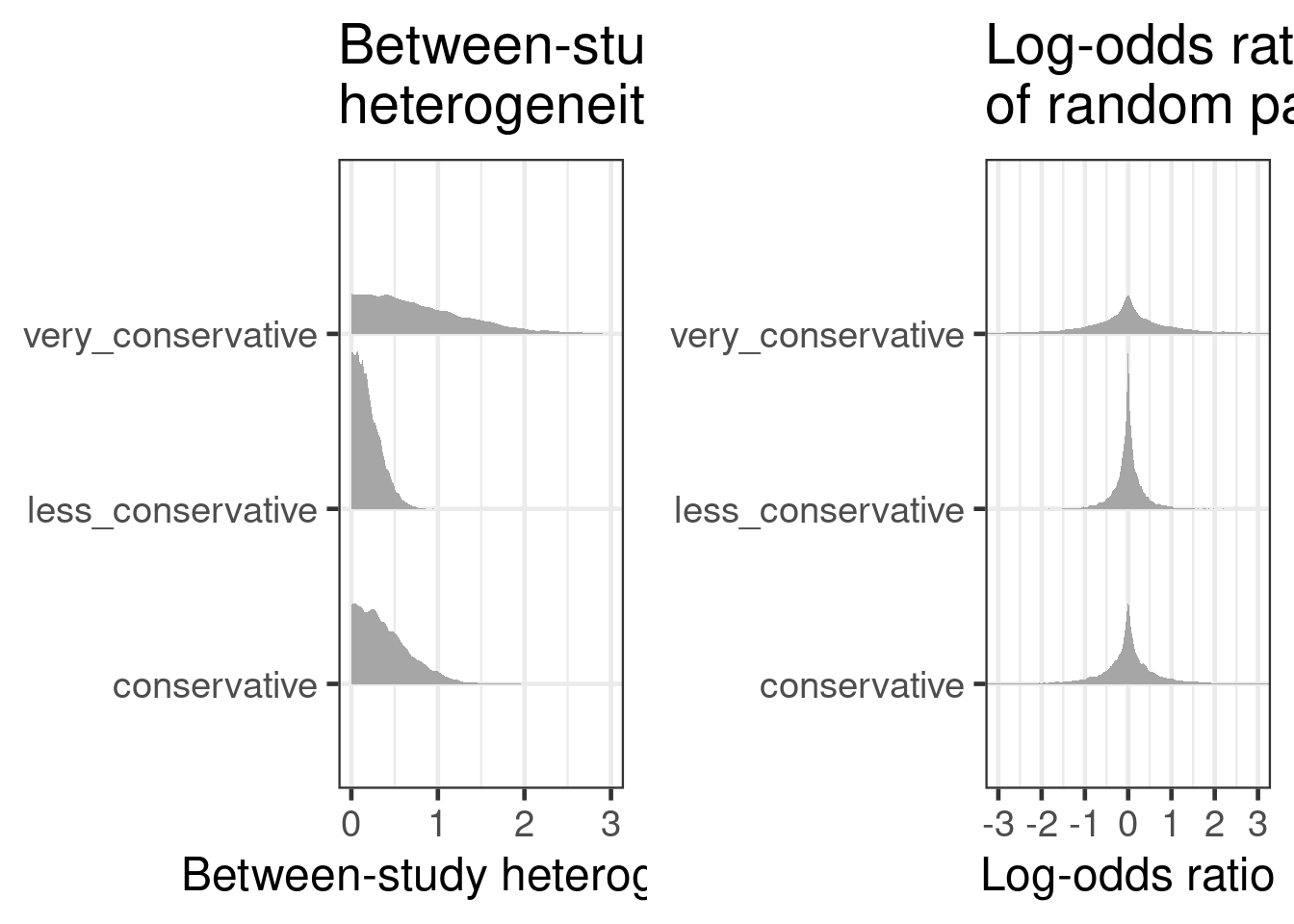
With the categorization of specific values for \(\tau\) we can now proceed and consider the interval probabilities for these categories for the different choices of \(\tau \sim \mbox{Normal}^+(s^2)\) for \(s=1\) and \(s=1/2\).

Show the code 
priors_cmp_tau <- tibble(case=c("less_conservative", "conservative", "very_conservative"),
                         density=c("HN(0, (1/4)^2)", "HN(0, (1/2)^2)", "HN(0, 1^2)"),
                         prior=rvar(cbind(abs(rnorm(num_draws, 0, 0.25)),
                                          abs(rnorm(num_draws, 0, 0.5)),
                                          abs(rnorm(num_draws, 0, 1))))
                         )

kable(priors_cmp_tau)
case density prior
less_conservative HN(0, (1/4)^2) 0.2 ± 0.15
conservative HN(0, (1/2)^2) 0.4 ± 0.30
very_conservative HN(0, 1^2) 0.8 ± 0.60
Show the code 
priors_hetero <- priors_cmp_tau |>
    ggplot(aes(y=case, xdist=prior)) +
    stat_slab() +
    xlab("Between-study heterogeneity") +
    ylab(NULL) +
    scale_x_continuous(breaks=0:3) +
    labs(title="Between-study\nheterogeneity") +
    coord_cartesian(xlim=c(0, 3))

priors_lor <- priors_cmp_tau |>
    mutate(lor1=rvar_rng(rnorm, n=n(), mean=0, prior),
           lor2=rvar_rng(rnorm, n=n(), mean=0, prior)) |>
    ggplot(aes(y=case, xdist=lor1-lor2)) +
    stat_slab() +
    xlab("Log-odds ratio") +
    ylab(NULL) +
    scale_x_continuous(breaks=-5:5) +
    labs(title="Log-odds ratio\nof random pair") +
    coord_cartesian(xlim=c(-3, 3))

bayesplot_grid(priors_hetero, priors_lor, grid_args=list(nrow=1))

Show the code 
tau_category <- function(tau) {
    fct_rev(cut(tau, c(0, 0.125, 0.25, 0.5, 1, Inf), labels=c("small", "moderate", "substantial", "large", "very_large")))
}

priors_cmp_tau |> unnest_rvars()|> 
    ggplot(aes(x=case, fill=tau_category(prior))) +
    geom_bar(position="fill") +
    xlab("Prior") +
    ylab("Probability") +
    labs(title="Prior interval probabilities", fill="Category") +
    ##scale_y_continuous(breaks=seq(0,1,by=0.2)) +
    theme(legend.position="right")

Show the code 
mutate(priors_cmp_tau,
       summarise_draws(prior,
                       small=~100*E(.x < 0.125),
                       moderate=~100*E( 0.125 <= .x & .x < 0.25 ),
                       substantial=~100*E( 0.25 <= .x & .x < 0.5 ),
                       large=~100*E( 0.5 <= .x & .x < 1 ),
                       very_large=~100*E( .x >= 1 )
                       )) |>
    select(case, density, small, moderate, substantial, large, very_large) |>
    kable(digits=1, caption="Interval probabilities per prior given in percent")
Interval probabilities per prior given in percent
case density small moderate substantial large very_large
less_conservative HN(0, (1/4)^2) 38.3 31.3 26.0 4.3 0.0
conservative HN(0, (1/2)^2) 19.7 18.9 29.9 26.9 4.6
very_conservative HN(0, 1^2) 9.6 9.9 18.6 30.1 31.8

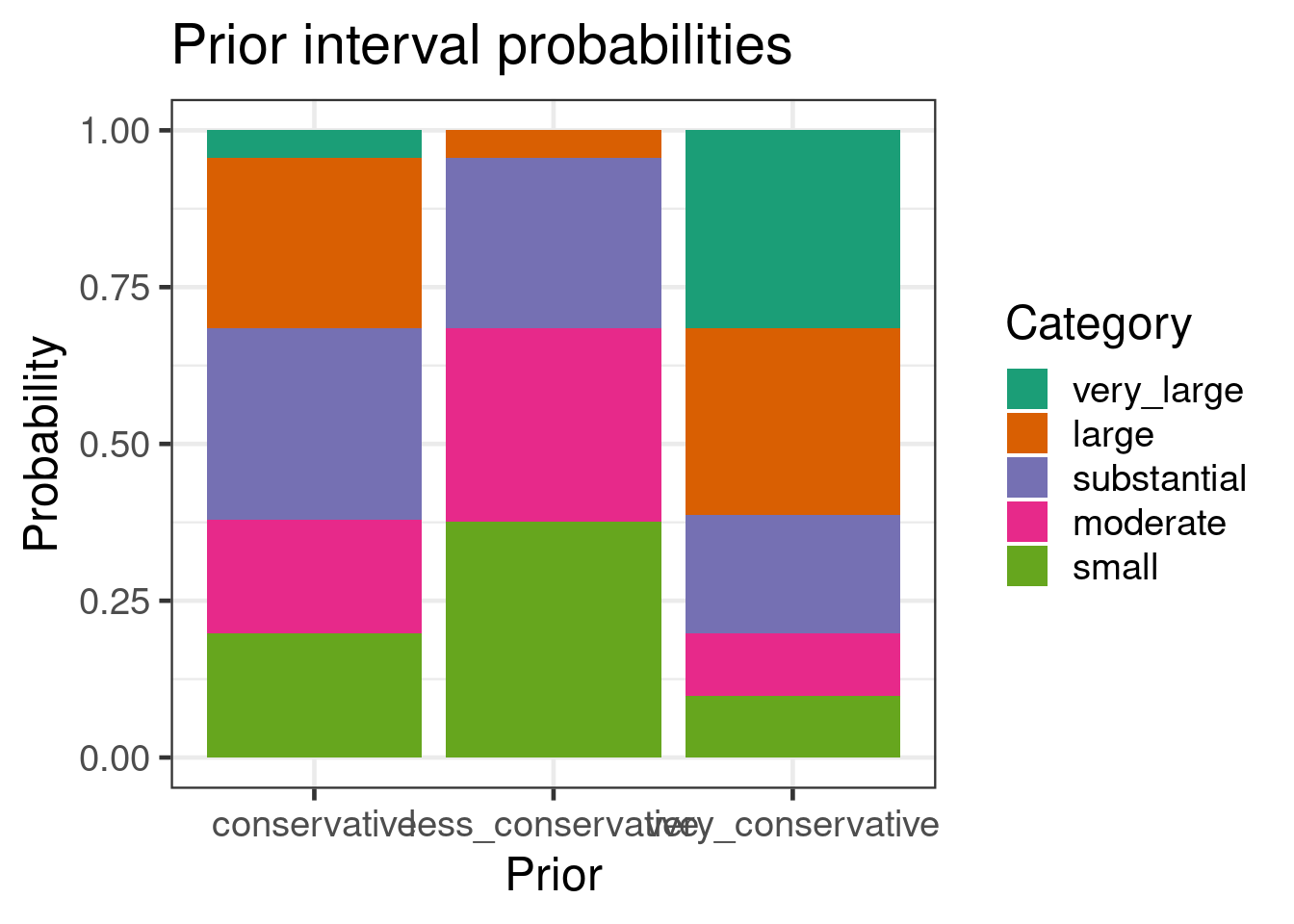
We can see that the “conservative” choice has an about 5% tail probability exceeding the value of large. This implies that some degree of homogeneity between the studies is given. This is usually the case whenever meta-analyses are conducted, since the inclusion & exclusion criteria for studies are aligned to a certain degree in order to ensure that a similar patient population is included in the analysis. In contrast, the “very conservative” choice admits with 30% probability mass the possibility of values in the domain “very large” for which practically no borrowing of historical information occurs. The “less conservative” choice on the hand has 5% tail probability above substantial. This way a large heterogeneity is considered to be unlikely as it can be the case for twin Phase III studies, for example.

Additional literature for consideration: