Skip to contents

Meta-Analytic-Predictive Analysis for Generalized Linear Models

Source: R/gMAP.R
gMAP.Rd

Meta-Analytic-Predictive (MAP) analysis for generalized linear models suitable for normal, binary, or Poisson data. Model specification and overall syntax follows mainly glm conventions.

Usage

gMAP(
  formula,
  family = gaussian,
  data,
  weights,
  offset,
  tau.strata,
  tau.dist = c("HalfNormal", "TruncNormal", "Uniform", "Gamma", "InvGamma", "LogNormal",
    "TruncCauchy", "Exp", "Fixed"),
  tau.prior,
  tau.strata.pred = 1,
  beta.prior,
  prior_PD = FALSE,
  REdist = c("normal", "t"),
  t.df = 5,
  contrasts = NULL,
  iter = getOption("RBesT.MC.iter", 6000),
  warmup = getOption("RBesT.MC.warmup", 2000),
  thin = getOption("RBesT.MC.thin", 4),
  init = getOption("RBesT.MC.init", 1),
  chains = getOption("RBesT.MC.chains", 4),
  cores = getOption("mc.cores", 1L)
)

# S3 method for class 'gMAP'
print(x, digits = 3, probs = c(0.025, 0.5, 0.975), ...)

# S3 method for class 'gMAP'
fitted(object, type = c("response", "link"), probs = c(0.025, 0.5, 0.975), ...)

# S3 method for class 'gMAP'
coef(object, probs = c(0.025, 0.5, 0.975), ...)

# S3 method for class 'gMAP'
as.matrix(x, ...)

# S3 method for class 'gMAP'
summary(
  object,
  type = c("response", "link"),
  probs = c(0.025, 0.5, 0.975),
  ...
)

Arguments

formula

the model formula describing the linear predictor and encoding the grouping; see details

family

the family of distributions defining the statistical model (binomial, gaussian, or poisson)

data

optional data frame containing the variables of the model. If not found in data, the variables are taken from environment(formula).

weights

optional weight vector; see details below.

offset

offset term in statistical model used for Poisson data

tau.strata

sets the exchangability stratum per study. That is, it is expected that each study belongs to a single stratum. Default is to assign all studies to stratum 1. See section differential heterogeniety below.

tau.dist

type of prior distribution for tau; supported priors are HalfNormal (default), TruncNormal, Uniform, Gamma, InvGamma, LogNormal, TruncCauchy, Exp and Fixed.

tau.prior

parameters of prior distribution for tau; see section prior specification below.

tau.strata.pred

the index for the prediction stratum; default is 1.

beta.prior

mean and standard deviation for normal priors of regression coefficients, see section prior specification below.

prior_PD

logical to indicate if the prior predictive distribution should be sampled (no conditioning on the data). Defaults to FALSE.

REdist

type of random effects distribution. Normal (default) or t.

t.df

degrees of freedom if random-effects distribution is t.

contrasts

an optional list; See contrasts.arg from model.matrix.default.

iter

number of iterations (including warmup).

warmup

number of warmup iterations.

thin

period of saving samples.

init

positive number to specify uniform range on unconstrained space for random initialization. See stan.

chains

number of Markov chains.

cores

number of cores for parallel sampling of chains.

x, object

gMAP analysis object created by gMAP function

digits

number of displayed significant digits.

probs

defines quantiles to be reported.

...

optional arguments are ignored

type

sets reported scale (response (default) or link).

Value

The function returns a S3 object of type gMAP. See the methods section below for applicable functions to query the object.

Details

The meta-analytic-predictive (MAP) approach derives a prior from historical data using a hierarchical model. The statistical model is formulated as a generalized linear mixed model for binary, normal (with fixed \(\sigma\)) and Poisson endpoints:

$$y_{ih}|\theta_{ih} \sim f(y_{ih} | \theta_{ih})$$

Here, \(i=1,\ldots,N\) is the index for observations, and \(h=1,\ldots,H\) is the index for the grouping (usually studies). The model assumes the linear predictor for a transformed mean as

$$g(\theta_{ih}; x_{ih},\beta) = x_{ih} \, \beta + \epsilon_h$$

with \(x_{ih}\) being the row vector of \(k\) covariates for observation \(i\). The variance component is assumed by default normal

$$\epsilon_h \sim N(0,\tau^2), \qquad h=1,\ldots,H$$

Lastly, the Bayesian implementation assumes independent normal priors for the \(k\) regression coefficients and a prior for the between-group standard deviation \(\tau\) (see taud.dist for available distributions).

The MAP prior will then be derived from the above model as the conditional distribution of \(\theta_{\star}\) given the available data and the vector of covariates \(x_{\star}\) defining the overall intercept

$$\theta_{\star}| x_{\star},y .$$

A simple and common case arises for one observation (summary statistic) per trial. For a normal endpoint, the model then simplifies to the standard normal-normal hierarchical model. In the above notation, \(i=h=1,\ldots,H\) and

$$y_h|\theta_h \sim N(\theta_h,s_h^2)$$ $$\theta_h = \mu + \epsilon_h$$ $$\epsilon_h \sim N(0,\tau^2),$$

where the more common \(\mu\) is used for the only (intercept) parameter \(\beta_1\). Since there are no covariates, the MAP prior is simply \(Pr(\theta_{\star} | y_1,\ldots,y_H)\).

The hierarchical model is a compromise between the two extreme cases of full pooling (\(\tau=0\), full borrowing, no discounting) and no pooling (\(\tau=\infty\), no borrowing, stratification). The information content of the historical data grows with H (number of historical data items) indefinitely for full pooling whereas no information is gained in a stratified analysis. For a fixed \(\tau\), the maximum effective sample size of the MAP prior is \(n_\infty\) (\(H\rightarrow \infty\)), which for a normal endpoint with fixed \(\sigma\) is

$$n_\infty = \left(\frac{\tau^2}{\sigma^2}\right)^{-1},$$

(Neuenschwander et al., 2010). Hence, the ratio \(\tau/\sigma\) limits the amount of information a MAP prior is equivalent to. This allows for a classification of \(\tau\) values in relation to \(\sigma\), which is crucial to define a prior \(P_\tau\). The following classification is useful in a clinical trial setting:

Heterogeneity\(\tau/\sigma\)\(n_\infty\)
small0.0625256
moderate0.12564
substantial0.2516
large0.54
very large1.01

The above formula for \(n_\infty\) assumes a known \(\tau\). This is unrealistic as the between-trial heterogeneity parameter is often not well estimable, in particular if the number of trials is small (H small). The above table helps to specify a prior distribution for \(\tau\) appropriate for the given context which defines the crucial parameter \(\sigma\). For binary and Poisson endpoints, normal approximations can be used to determine \(\sigma\). See examples below for concrete cases.

The design matrix \(X\) is defined by the formula for the linear predictor and is always of the form response ~ predictor | grouping, which follows glm conventions. The syntax has been extended to include a specification of the grouping (for example study) factor of the data with a horizontal bar, |. The bar separates the optionally specified grouping level, i.e. in the binary endpoint case cbind(r, n-r) ~ 1 | study. By default it is assumed that each row corresponds to an individual group (for which an individual parameter is estimated). Specifics for the different endpoints are:

normal

family=gaussian assumes an identity link function. The response should be given as matrix with two columns with the first column being the observed mean value \(y_{ih}\) and the second column the standard error \(se_{ih}\) (of the mean). Additionally, it is recommended to specify with the weight argument the number of units which contributed to the (mean) measurement \(y_{ih}\). This information is used to estimate \(\sigma\).

binary

family=binomial assumes a logit link function. The response must be given as two-column matrix with number of responders \(r\) (first column) and non-responders \(n-r\) (second column).

Poisson

family=poisson assumes a log link function. The response is a vector of counts. The total exposure times can be specified by an offset, which will be linearly added to the linear predictor. The offset can be given as part of the formula, y ~ 1 + offset(log(exposure)) or as the offset argument to gMAP. Note that the exposure unit must be given as log-offset.

Methods (by generic)

  • print(gMAP): displays a summary of the gMAP analysis.

  • fitted(gMAP): returns the quantiles of the posterior shrinkage estimates for each data item used during the analysis of the given gMAP object.

  • coef(gMAP): returns the quantiles of the predictive distribution. User can choose with type if the result is on the response or the link scale.

  • as.matrix(gMAP): extracts the posterior sample of the model.

  • summary(gMAP): returns the summaries of a gMAP. analysis. Output is a gMAPsummary object, which is a list containing

    tau

    posterior summary of the heterogeneity standard deviation

    beta

    posterior summary of the regression coefficients

    theta.pred

    summary of the predictive distribution (given in dependence on the type argument either on response or link scale)

    theta

    posterior summary of the mean estimate (also depends on the type argument)

Differential Discounting

The above model assumes the same between-group standard deviation \(\tau\), which implies that the data are equally relevant. This assumption can be relaxed to more than one \(\tau\). That is,

$$\epsilon_h \sim N(0,\tau_{s(h)}^2)$$

where \(s(h)\) assignes group \(h\) to one of \(S\) between-group heterogeneity strata.

For example, in a situation with two randomized and four observational studies, one may want to assume \(\tau_1\) (for trials 1 and 2) and \(\tau_2\) (for trials 3-6) for the between-trial standard deviations of the control means. More heterogeneity (less relevance) for the observational studies can then be expressed by appropriate priors for \(\tau_1\) and \(\tau_2\). In this case, \(S=2\) and the strata assignments (see tau.strata argument) would be \(s(1)=s(2)=1, s(3)=\ldots=s(6)=2\).

Prior Specification

The prior distribution for the regression coefficients \(\beta\) is normal.

  • If a single number is given, then this is used as the standard deviation and the default mean of 0 is used.

  • If a vector is given, it must be of the same length as number of covariates defined and is used as standard deviation.

  • If a matrix with a single row is given, its first row will be used as mean and the second row will be used as standard deviation for all regression coefficients.

  • Lastly, a two-column matrix (mean and standard deviation columns) with as many columns as regression coefficients can be given.

It is recommended to always specify a beta.prior. Per default a mean of 0 is set. The standard deviation is set to 2 for the binary case, to 100 * sd(y) for the normal case and to sd(log(y + 0.5 + offset)) for the Poisson case.

For the between-trial heterogeniety \(\tau\) prior, a dispersion parameter must always be given for each exchangeability stratum. For the different tau.prior distributions, two parameters are needed out of which one is set to a default value if applicable:

Prior\(a\)\(b\)default
HalfNormal\(\mu = 0\)\(\sigma\)
TruncNormal\(\mu\)\(\sigma\)\(\mu = 0\)
Uniformaba = 0
Gamma\(\alpha\)\(\beta\)
InvGamma\(\alpha\)\(\beta\)
LogNormal\(\mu_{\log}\)\(\sigma_{\log}\)
TruncCauchy\(\mu\)\(\sigma\)\(\mu = 0\)
Exp\(\beta\)0
Fixeda0

For a prior distribution with a default location parameter, a vector of length equal to the number of exchangability strata can be given. Otherwise, a two-column matrix with as many rows as exchangability strata must be given, except for a single \(\tau\) stratum, for which a vector of length two defines the parameters a and b.

Random seed

The MAP analysis is performed using Markov-Chain-Monte-Carlo (MCMC) in rstan. MCMC is a stochastic algorithm. To obtain exactly reproducible results you must use the set.seed function before calling gMAP. See RBesT overview page for global options on setting further MCMC simulation parameters.

References

Neuenschwander B, Capkun-Niggli G, Branson M, Spiegelhalter DJ. Summarizing historical information on controls in clinical trials. Clin Trials. 2010; 7(1):5-18

Schmidli H, Gsteiger S, Roychoudhury S, O'Hagan A, Spiegelhalter D, Neuenschwander B. Robust meta-analytic-predictive priors in clinical trials with historical control information. Biometrics 2014;70(4):1023-1032.

Weber S, Li Y, Seaman III J.W., Kakizume T, Schmidli H. Applying Meta-Analytic Predictive Priors with the R Bayesian evidence synthesis tools. JSS 2021; 100(19):1-32

See also

plot.gMAP, forest_plot, automixfit, predict.gMAP

Examples

## Setting up dummy sampling for fast execution of example
## Please use 4 chains and 20x more warmup & iter in practice
.user_mc_options <- options(RBesT.MC.warmup=50, RBesT.MC.iter=100,
                            RBesT.MC.chains=2, RBesT.MC.thin=1)

# Binary data example 1

# Mean response rate is ~0.25. For binary endpoints
# a conservative choice for tau is a HalfNormal(0,1) as long as
# the mean response rate is in the range of 0.2 to 0.8. For
# very small or large rates consider the n_infinity approach
# illustrated below.
# for exact reproducible results, the seed must be set
set.seed(34563)
map_AS <- gMAP(cbind(r, n-r) ~ 1 | study,
               family=binomial,
               data=AS,
               tau.dist="HalfNormal", tau.prior=1,
               beta.prior=2)
#> Assuming default prior location   for beta: 0
#> Warning: The largest R-hat is 1.11, indicating chains have not mixed.
#> Running the chains for more iterations may help. See
#> https://mc-stan.org/misc/warnings.html#r-hat
#> Warning: Bulk Effective Samples Size (ESS) is too low, indicating posterior means and medians may be unreliable.
#> Running the chains for more iterations may help. See
#> https://mc-stan.org/misc/warnings.html#bulk-ess
#> Warning: Tail Effective Samples Size (ESS) is too low, indicating posterior variances and tail quantiles may be unreliable.
#> Running the chains for more iterations may help. See
#> https://mc-stan.org/misc/warnings.html#tail-ess
#> Warning: Maximal Rhat > 1.1. Consider increasing RBesT.MC.warmup MCMC parameter.
#> Final MCMC sample equivalent to less than 1000 independent draws.
#> Please consider increasing the MCMC simulation size.
print(map_AS)
#> Generalized Meta Analytic Predictive Prior Analysis
#> 
#> Call:  gMAP(formula = cbind(r, n - r) ~ 1 | study, family = binomial, 
#>     data = AS, tau.dist = "HalfNormal", tau.prior = 1, beta.prior = 2)
#> 
#> Exchangeability tau strata: 1 
#> Prediction tau stratum    : 1 
#> Maximal Rhat              : 1.11 
#> 
#> Between-trial heterogeneity of tau prediction stratum
#>  mean    sd  2.5%   50% 97.5% 
#> 0.370 0.163 0.110 0.352 0.764 
#> 
#> MAP Prior MCMC sample
#>   mean     sd   2.5%    50%  97.5% 
#> 0.2580 0.0817 0.1230 0.2510 0.4460 
#> Warning: Parts of the model have not converged (some Rhats are > 1.1).
#> Be careful when analysing the results! It is recommend to run
#> more iterations and/or setting stronger priors.

# obtain numerical summaries
map_sum <- summary(map_AS)
print(map_sum)
#> Heterogeneity parameter tau per stratum:
#>        mean    sd 2.5%   50% 97.5%
#> tau[1] 0.37 0.163 0.11 0.352 0.764
#> 
#> Regression coefficients:
#>              mean    sd  2.5%   50%  97.5%
#> (Intercept) -1.12 0.178 -1.47 -1.11 -0.767
#> 
#> Mean estimate MCMC sample:
#>             mean    sd  2.5%   50% 97.5%
#> theta_resp 0.248 0.033 0.187 0.247 0.317
#> 
#> MAP Prior MCMC sample:
#>                  mean     sd  2.5%   50% 97.5%
#> theta_resp_pred 0.258 0.0817 0.123 0.251 0.446
names(map_sum)
#> [1] "tau"        "beta"       "theta.pred" "theta"     
# [1] "tau"        "beta"       "theta.pred" "theta"
map_sum$theta.pred
#>                      mean         sd      2.5%       50%     97.5%
#> theta_resp_pred 0.2576768 0.08166927 0.1232554 0.2508299 0.4464658

# \donttest{
# graphical model checks (returns list of ggplot2 plots)
map_checks <- plot(map_AS)
# forest plot with shrinkage estimates
map_checks$forest_model

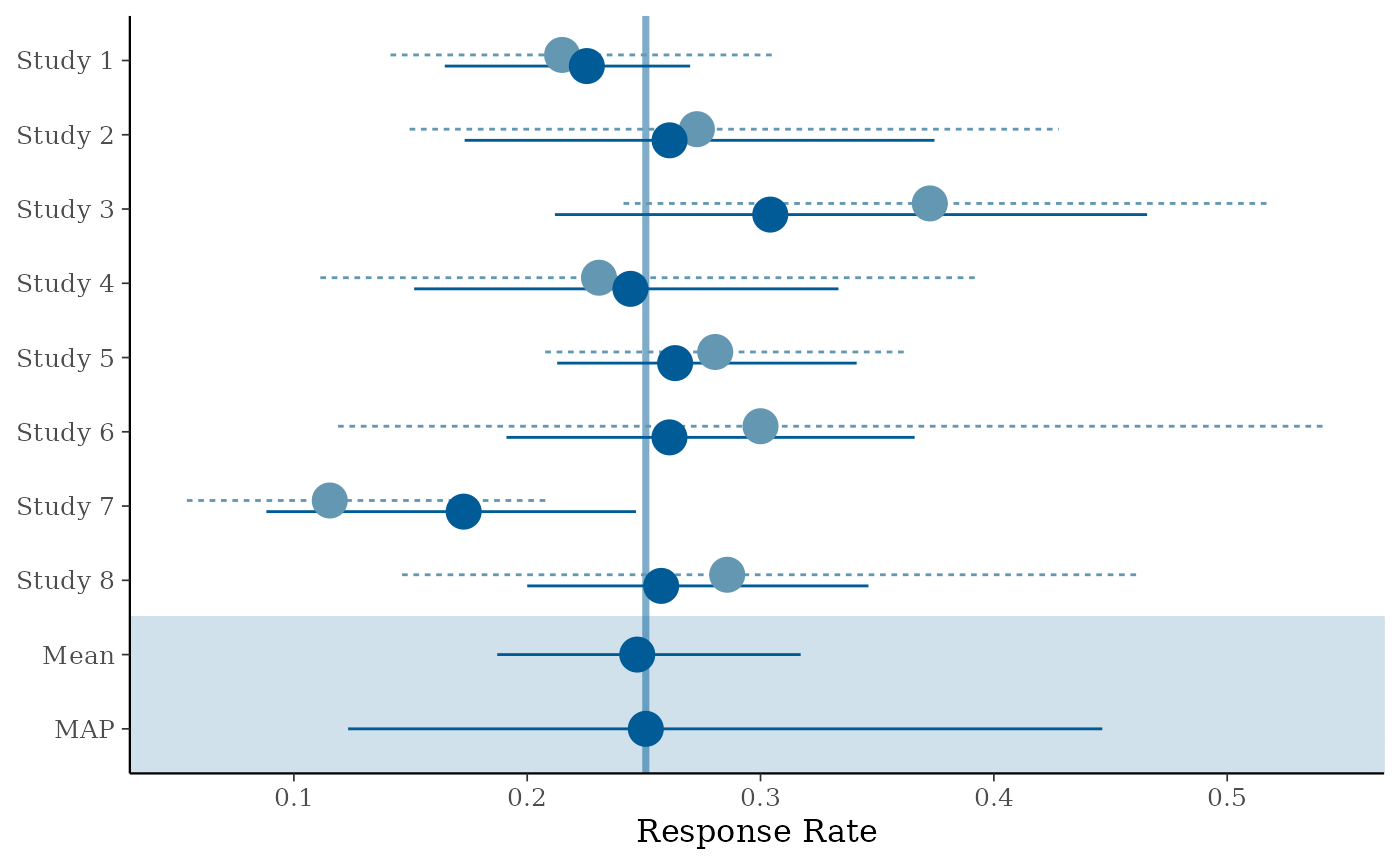# density of MAP prior on response scale
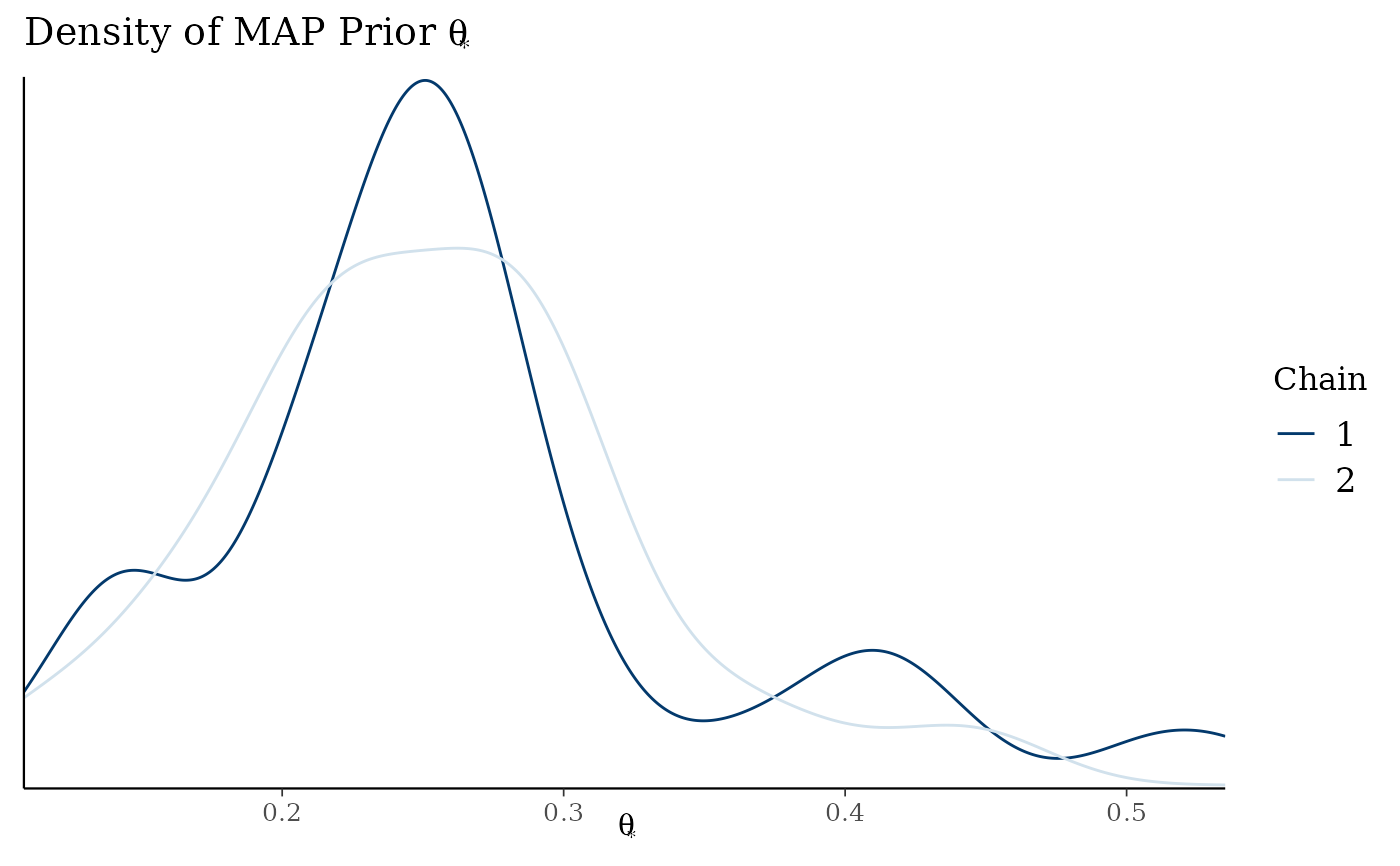
map_checks$densityThetaStar

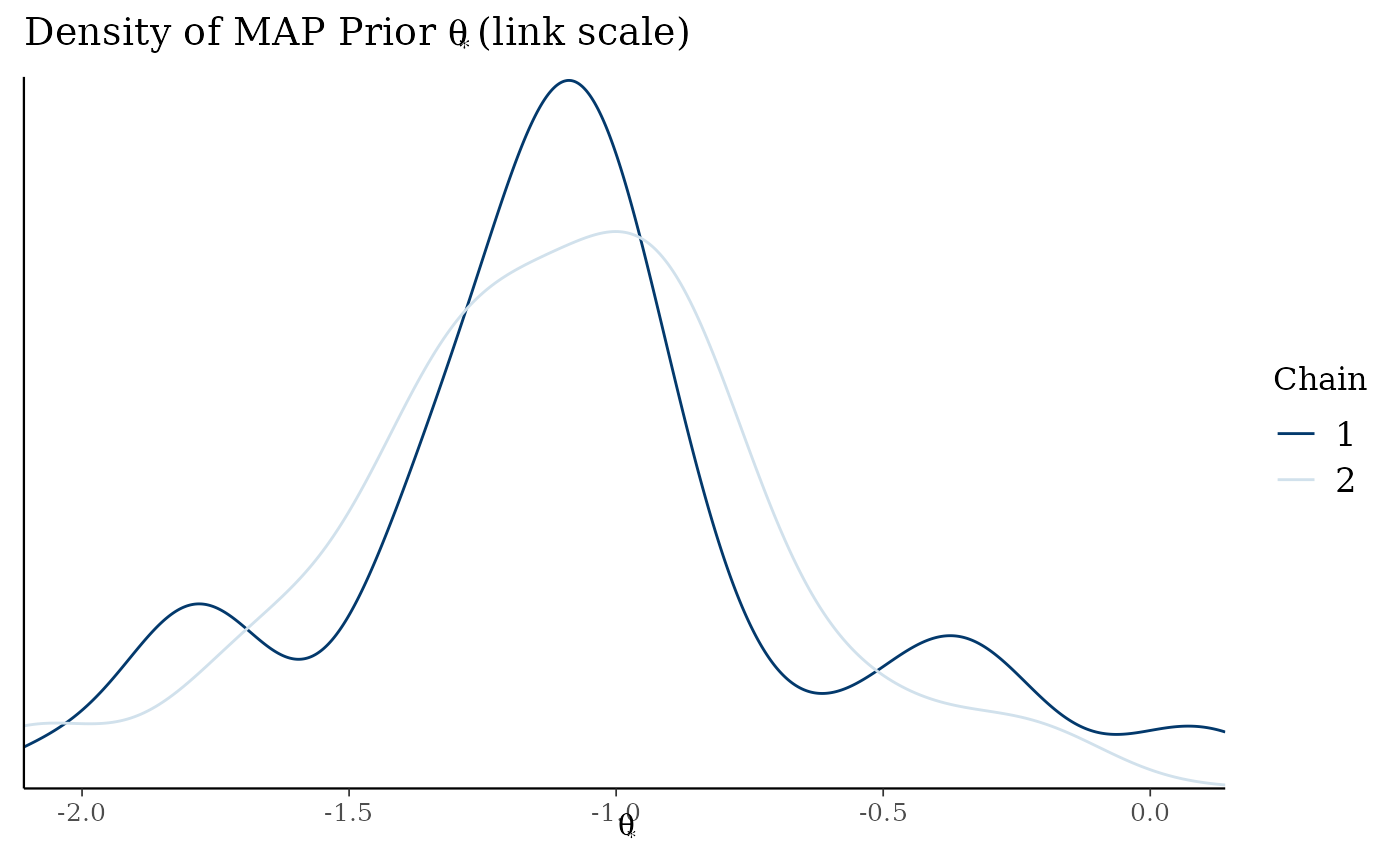
# density of MAP prior on link scale
map_checks$densityThetaStarLink

# }

# obtain shrinkage estimates
fitted(map_AS)
#>              mean         sd       2.5%       50%     97.5%
#> Study 1 0.2245230 0.03009877 0.16467408 0.2255518 0.2698386
#> Study 2 0.2600974 0.05160094 0.17318985 0.2610201 0.3745415
#> Study 3 0.3157218 0.06628311 0.21188389 0.3041774 0.4656744
#> Study 4 0.2440305 0.04812868 0.15154707 0.2442546 0.3333963
#> Study 5 0.2681039 0.03179363 0.21285005 0.2633981 0.3412085
#> Study 6 0.2670423 0.05109495 0.19112391 0.2609730 0.3660353
#> Study 7 0.1704818 0.04185255 0.08821842 0.1727647 0.2466163
#> Study 8 0.2649455 0.04246509 0.20001270 0.2574109 0.3462487

# regression coefficients
coef(map_AS)
#>                 mean        sd      2.5%       50%      97.5%
#> (Intercept) -1.11748 0.1782488 -1.468582 -1.113787 -0.7667301

# finally fit MAP prior with parametric mixture
map_mix <- mixfit(map_AS, Nc=2)
plot(map_mix)$mix


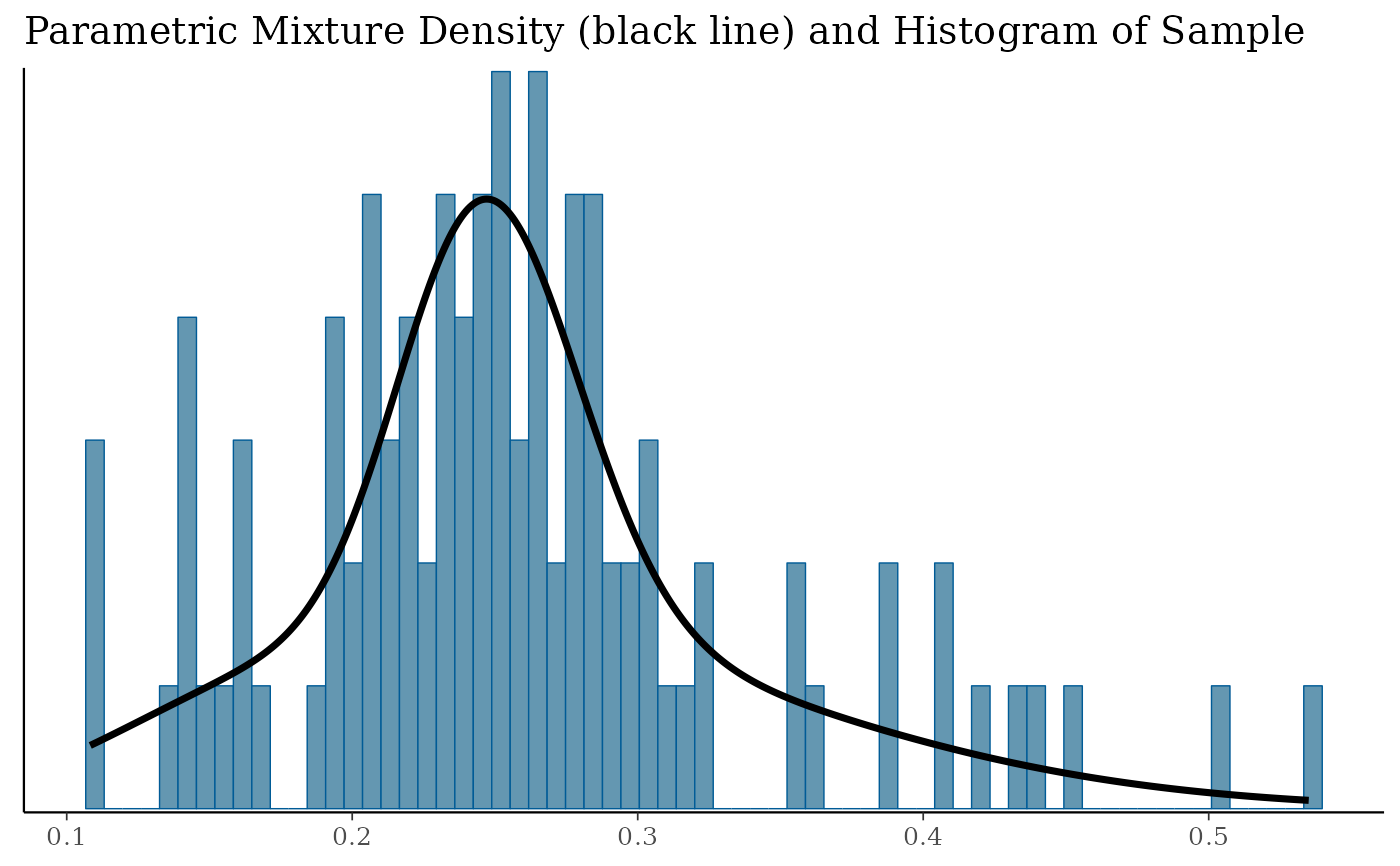# \donttest{
# optionally select number of components automatically via AIC
map_automix <- automixfit(map_AS)
plot(map_automix)$mix

# }

# Normal example 2, see normal vignette

# Prior considerations

# The general principle to derive a prior for tau can be based on the
# n_infinity concept as discussed in Neuenschwander et al., 2010.
# This assumes a normal approximation which applies for the colitis
# data set as:
p_bar <- mean(with(colitis, r/n))
s <- round(1/sqrt(p_bar * (1-p_bar)), 1)
# s is the approximate sampling standard deviation and a
# conservative prior is tau ~ HalfNormal(0,s/2)
tau_prior_sd <- s/2

# Evaluate HalfNormal prior for tau
tau_cat <- c(pooling=0
            ,small=0.0625
            ,moderate=0.125
            ,substantial=0.25
            ,large=0.5
            ,veryLarge=1
            ,stratified=Inf)
# Interval probabilites (basically saying we are assuming
# heterogeniety to be smaller than very large)
diff(2*pnorm(tau_cat * s, 0, tau_prior_sd))
#>       small    moderate substantial       large   veryLarge  stratified 
#>  0.09947645  0.09793620  0.18551227  0.29976457  0.27181024  0.04550026 
# Cumulative probabilities as 1-F
1 - 2*(pnorm(tau_cat * s, 0, tau_prior_sd) - 0.5)
#>     pooling       small    moderate substantial       large   veryLarge 
#>  1.00000000  0.90052355  0.80258735  0.61707508  0.31731051  0.04550026 
#>  stratified 
#>  0.00000000 

## Recover user set sampling defaults
options(.user_mc_options)