Error Models

On this page

Error Models#

UNIQUE also supports the generation of ML models to predict the error of the original model.

These so-called error models have been proposed in previous works[1] to predict both the absolute and squared differences between predicted and observed values.

UNIQUE’s error models are predictive models that are trained to predict up to three different types of prediction errors:

  • "L1" error (defined as \(|y - \hat{y}|\));

  • "L2" error (defined as \((y - \hat{y})^2\));

  • "unsigned" error (defined as \(y - \hat{y}\));

where \(y = label\) and \(\hat{y} = prediction\).

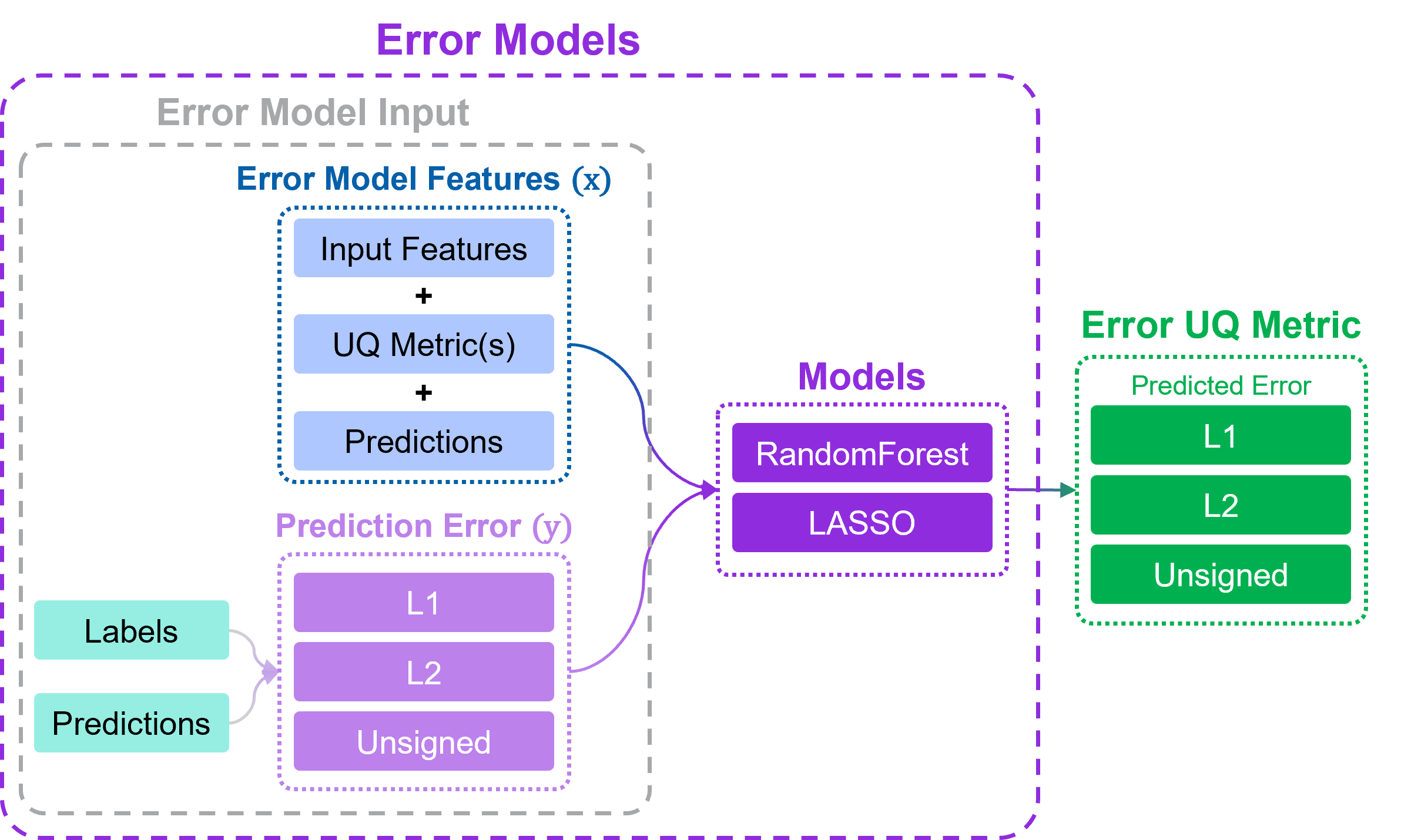
UNIQUE Error Model Schema

Detailed workflow schema for UNIQUE’s error models.#

Given the original input features, along with computed UQ values, UNIQUE generates three different sets of input features to train the error predictors:

  1. Original model’s prediction, UQ methods, and original input features provided by the user;

  2. Original model’s prediction and UQ methods only;

  3. Original model’s prediction and non-transformed UQ methods only.

The samples are taken from the "TRAIN" and "CALIBRATION" subsets only; the "TEST" subset is left aside to ensure proper validation.

UNIQUE currently supports two predictive algorithms: Least Absolute Shrinkage and Selection Operator (LASSO)[2], and Random Forest (RF)[3]. Both rely on their respective scikit-learn implementations for the hyperparameters definition (i.e., it is possible to specify any supported kwargs in the configuration file).

Error models are a special case of UQ methods themselves, and their predicted errors can be regarded as UQ values and evaluated as such in UNIQUE’s benchmark. In UNIQUE they are considered as transformed UQ methods, as they are generated from a further transformation/processing of other UQ methods.

See also

Check out Available Inputs & UQ Methods for more details about error models.

References#

On this page